Tema2

TEMA 2

Primero, debemos definir los conceptos de Criptografía y de Criptoanálisis:

Criptografía : "arte" de ocultar la información, aunque sea visible.

Criptoanálisis: técnicas para averiguar la información criptográfica, sin conocer la técnica de la Criptografía. Depende de la criptografía utilizada y de los datos adicionales.

Un método criptográfico tiene que poder transformar, la información, en otra ilegible y además se pueda deshacer este cambio, si la otra persona esta autorizada.
Para poder cifrar y descifrar de forma legal se necesita una "llave" o "clave"( key ), sin esta clave no se debe poder descifrar la información.

Criptosistema:

Es una quíntupla formada por estos elementos:

M : Todos los posibles mensajes que se puedan cifrar.
C : Todos los mensajes cifrados.
K : Todas las posibles claves.
E : Conjunto de las transformaciones de cifrado.
D : Conjunto de las transformaciones de descifrado.

Un criptosistema es utilizable si y sólo si E_k(m)=c; D_k(c)=m
Hay dos grandes tipos :

De clave privada : más sencillos y antiguos, sólo hay una clave para cifrar y descifrar, por eso se llaman también simétricos.
De clave publica : hay dos claves, una publica y otra privada, por eso también se llaman asimétricos, las claves van por pares ( una privada con una publica ), la clave privada se mantiene en secreto y la publica se da a conocer. Son muy costosos de implementar y un coste algorítmico muy alto. Aparecen en 1976, el primer algoritmo conocido es el Riverst-Shamir-Adelman( RSA ).

Ahora pasamos a definir el termino Entropía:
En el 48 Shanon, publicó: la teoría matemática de la información, donde aparece esta propiedad. No se sabe muy bien que es, pero aumenta en los procesos energéticos. Es una medid del desorden.
La entropía en la información, va enfocada al desorden y a la "uniformización". Diremos que hay algo imprevisible y le llamaremos entrópico, si no se conoce muy bien lo que puede pasar.

Redundancia de un lenguaje: la entropía de un mensaje, partido el tamaño del mensaje(K).
Indice Real: r_k=H_k(M) / k M:conjunto de todos los mensajes
Indice absoluto R=log₂(m) m:número de letras
Redundancia: D=R-r_k
_{Máxima compresión=
D/R.}

Cantidad de información que 'x' contiene sobre 'y'.
    I(X,Y) = H(Y) - H(Y/X)
Criptosistema seguro de Shanon o ideal.
    I(C,M) = 0
Para que esto se cumpla el cardinal de las claves debe de ser como mínimo igual al cardinal del numero de mensajes. En la práctica es 'casi' imposible de realizar.
Desinformación de un sistema :
    H(M/C) si H(M) = H(M/C) criptosistema ideal
Longitud mínima de mensaje cifrado que lleva H(K/C) a cero, la cantidad mínima de mensaje para conocer la clave.

Técnicas básicas para ocultar redundancia :

Confusión : Intenta ocultar la relación entre C y M y el mecanismo más simple es la sustitución, este consiste en sustituir un símbolo por otro.

Difusión : Consiste en diluir la redundancia, repartiendol a por todo el texto, esto se consigue por transposición, que quiere decir cambiar las cosas de sitio.

Algunos de los conceptos que se utilizan son los siguientes:

Aritmética modular: Trabaja con conjuntos de signos determinados.

n= número de modulo, a,b,c otros números

a,b,n pertenecen a los naturales.

'a' equivalente a 'b' (mod n) si a = b + kn

'm' divide a 'a' ( m|a )

Esto nos sirve para conocer los números primos entre si. Dos números 'a' y 'n' son primos entre si, si el máximo común divisor de 'a' y 'n', mcd(a,n), es el 1, esto quiere decir que 'a' tiene inversa en modulo 'n' (a^-1) : a·a^-1=1 ( mod n )

Conjunto de residuos( en mod n ): todos lo números del conjunto.

CR={ 1,2,3,4,..., n-2,n-1}

Conjunto de residuos reducido( en mod n ): todos los números primos entre si.

CRR( de n=12 )={ 1,5,7,11 }

Cardinal del CRR= función de Euler

Teorema

mcd(a,n)=1

a =1 ( mod n )

El teorema anterior se utiliza para realizar el algoritmo de exponenciación rápida y este a su vez se utiliza para el cifrado, como los conceptos que ahora describiremos.
No se conoce ninguna formula que calcule números primos, pero si que se pueden intentar conocer por la fuerza bruta, según este método para conocer si un número es primo se divide por 2 y luego por los números impares hasta la raíz cuadrada del mismo. Otro método es el test de Lehmann ( ejemplo ) :
    Se quiere saber si 'p' es primo
    a<p
    b=a ( mod p )
    Si b distinto de 1 y de p-1 entonces no es primo, sino 50% + efectivo.

Para conseguir un número primo se crea un número muy gordo y se le saca un '1' al principio y luego se 'divide' por los números primos que hay entre el 1..2000 y para terminar se le aplica el test de Lehmann de 10 a 20 veces.

Otra definición importante es la de primos fuertes:

Dos números p,q son primos fuertes si:

mcd[(p-1),(p-1)] es pequeño.
p-1 y p-1 tienen algún factor primo muy grande (p', q').
p'-1 y q'-1 tienen algún factor primo muy grande.
p'+1 y q'+1 tienen algún factor primo muy grande.

Para obtener una secuencia de números aleatorios, se puede obtener el primer valor de la secuencia mediante un 'ruido'(ej: randomize(time(NULL)).

Los sistemas de cifrado clásicos son poco viables para la seguridad computacional pero nos dan una idea bastante clara de como funciona el concepto de cifrado.

Método de la vara de mando, en este método se necesita tener una vara con igual tamaño que la original para poder descifrar el mensaje( la clave, sería el tamaño de la vara ).
Método Cesar, creado por Julio Cesar, es un método de cifrado por sustitución, a continuación veremos un ejemplo con clave 3 :

A	B	C	D	E	...	V	W	X	Y	Z
D	E	F	G	H	...	Y	Z	A	B	C

HOLA se transforma en KROD.

Método Vigenere( o polialfabético ), en este método se cifra como en el anterior pero variando la clave según el carácter que se ha de cifrar, a continuación veremos un ejemplo con clave 3,6,2:

A	B	C	D	E	F	...	W	X	Y	Z
D	E	F	G	H	I	...	Z	A	B	C
G	H	I	J	K	L	...	C	D	E	F
C	D	E	F	G	H	...	Y	Z	A	B

AVE se transforma en DBG.

Método de transposición, este método cifra por bloques, cada bloque se cifra según un vector de transposición el cual es la clave, a continuación veremos un ejemplo.

Vector de transposición

'Hola como estas.' se transforma en 'lac Hoo seoms. ta'

Ahora pasaremos a hablar sobre el cifrado moderno( computacional ) el primer algoritmo que observaremos es el DES, que funciona de la siguiente manera :

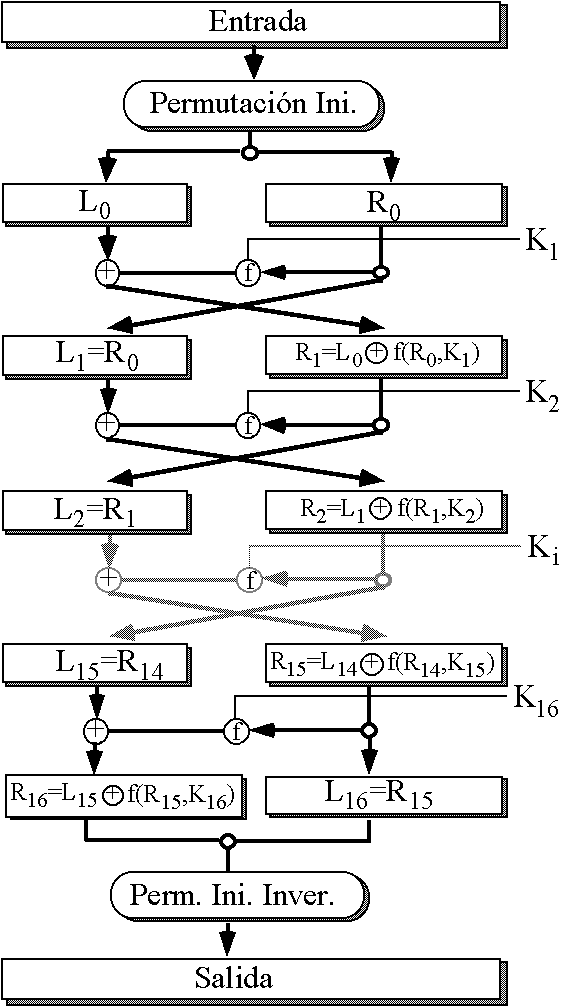
ECB( Electronic Code Block )

En modo ECB el texto en claro es dividido en bloques de 8 bytes que se cifran uno a uno y por separado usando el DES. La concatenación de los bloques cifrados da lugar al texto cifrado.
Este modo tiene el problema de que puede aparecer una información, que se pretendía tener oculta, dado que el los bloques iguales se cifran de igual forma generando información redundante.

CBC( Cifer Block Chaining )

En este modo, antes de cifrar cada bloque de 8 bytes, se le aplica una XOR sobre el bloque cifrado anterior. El primer bloque se combina con un valor conocido, vector de inicialización. De este modo, se produce un encadenamiento entre los distintos bloques, y el resultado de cifrar cada uno de ellos depende de todos los anteriores.
En este modo de funcionamiento un error en el texto cifrado tan solo afecta al descifrado de dos bloques. A continuación veremos como funciona el CBC, IV es el vector de inicialización.

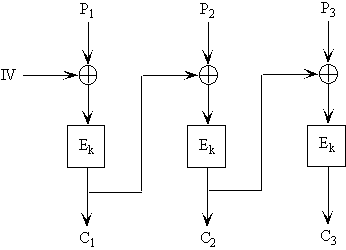
CFB( Cifer FeedBack )

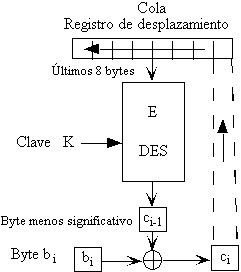
En este modo se mantiene una cola de caracteres. Se cifran bloques sucesivos de 8 bytes de la cola. El byte más significativo del resultado se combina (XOR) con el siguiente byte en claro para dar lugar al byte cifrado a transmitir. Además este último byte se reintroduce en la cola provocando un desplazamiento de su contenido.

Este método permite descifrar cualquier parte del texto cifrado sin conocer el resto. Además, este modo realiza el cifrado a nivel de carácter, de modo que el texto cifrado va surgiendo de modo flujo (stream mode) y no por bloques.

Ahora hablaremos de RSA, un algoritmo de clave pública, este algoritmo es unas 1000 veces mas lento que el DES y además facilita la Criptología, puesto que se pueden crear textos cifrado. Pero tiene la ventaja de que la clave es pública y por lo tanto cualquier puede enviarte información cifrada, de una forma bastante segura.
Ahora hablaremos de su funcionamiento, se basa en una serie de propiedades teóricas de la aritmética modular y de los números enteros, lo que lo convierte en un algoritmo bastante robusto y consistente. El primer principio en el que se basa es el siguiente,
siendo 'e', un número pequeño, el inverso de 'd', un bastante grande y =(p-1)·(q-1) donde 'p' y 'q' son primos fuertes. Teniendo este par de números el cifrado se consigue de la siguiente forma donde 's' es el cifrado y 'M' es el mensaje y el descifrado de esta otra .

En estas lineas hablaremos sobre la firma electrónica o digital, la firma electrónica tiene la misma función que la firma analógica, esta es la de verificar la identidad del emisor del mensaje, y además también la de proteger los datos, para esto en informática se utilizan los algoritmos de clave pública con el par de claves, de la siguiente forma :

Para obtener confidencialidad se utilizan las siguientes formulas C=E_P_B(m) y D_K_B(C)=D_K_B(E_P_A(m))=m
Para obtener la autenticidad se utilizan estas dos C=E_K_A(m) y D_P_A(C)=D_P_A(E_K_A(m))=m

Pero estos algoritmos producen dos problemas, uno de ellos es la poca certeza que tiene una clave pública, puesto que no se puede estar seguro, de si realmente el que dice ser su propietario, es su propietario. El segundo y más importante es la lentitud del algoritmo, pero este problema tiene fácil solución, esta es la utilización de una llave de sesión, la cual agiliza los cálculos. Ahora la confidencialidad quedaría de esta forma D_S(E_S(m))=m y D_K_B(E_P_B(S))=m.
Otra forma de implementar un firma digital es mediante una función de resumen( Hash ). En estas funciones se introduce el mensaje 'm' para el que se obtiene una salida 'C', ahora si el mensaje sufre alguna modificación la salida 'C' anterior debe de cambiar totalmente de forma, otro objetivo que debe cumplir la función de resumen, es el de imposibilitar que se pueda encontrar un texto que genere la misma 'C' que otro. La función de resumen debe de trabajar de esta forma :

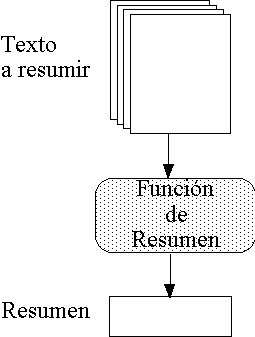
Para solucionar el problema de la falta de certeza, por parte del emisor se pueden utilizar dos soluciones, que son la siguientes :

Esta es la más fácil, pero también la menos factible y es la de realizar la entrega de la clave de forma física, o sea, darle a la otra persona un papel con la clave, decir se la por teléfono,...
Esta es la más usada y esta basada en la confianza, en esta segunda se utilizan notarios digitales( Autoridades Certificadoras, CA ), que nos confirman que la clave es realmente de la persona que dice que es suya, si un usuario quiere invalidar su firma, le dice al CA, que revoque su clave.

Para realizar la segunda opción, se utilizan los certificados, que son unos registros que contienen datos sobre el propietario de la firma, su organización, el país,... Estos certificados son un standard, el ISO X509.
Los certificados de una CA, se llaman certificados autofirmados o sea que se ha formado con la clave privada de la clave pública que hay en el certificado. Pero para estar completamente seguro del remitente, se debería verificar la CA, estos se puede hacer físicamente, es decir ir en persona a hablar con la CA o bien como se hace, teniendo incluidas las CA en el software de navegación. Este es uno de los puntos débiles de este método.

Por último hablaremos de los estándares RSA, o los PCKS, primero para conseguir un certificado se deben de dar los datos personales, seguidamente se debe elegir su formato y por último se deben de generar un par de llaves( recomendado, generadas por el usuario ). Después la CA valida los datos del usuario, DN, y genera el certificado, incluyendo un distintivo suyo, para que se pueda validar que el certificado ha sido realmente creado por esa CA.
Si una persona quiere anular un certificado, o pierde la clave del mismo puede revocar el certificado, cuando se realiza esta acción se guarda tu DN con un número de serie, en el CRL(Certificate Revocate List), donde se encuentran todos los certificados revocados.