Tema 2
Fundamentos de criptografía
 

2.1 Teoría de la información

De los objetivos del tema 1, hay una herramienta que ayuda concretamente a la confidencialidad, esta herramienta es la criptología. La criptología se puede descomponer en dos campos que son el campo de la criptografía y el campo del criptoanálisis.

La criptografía es el “arte” de ocultar la información, es una ciencias de carácter histórico. Consiste en una serie de métodos que transforman la información en otra información que no permite su comprensión.

El criptoanálisis esta formado por una serie de técnicas que intentan descifrar una información encriptada de una forma no lícita ( desde el punto de vista técnico).

El criptoanálisis desde un punto de vista legal puede ser correcto o no, dependerá de cómo haya sido cifrado y de la información adicional de la que dispongamos en ese momento.

Siempre será mejor trabajar con secuencias largas de criptografía, ya que a una mayor cantidad de información mayor será la cantidad de cifrado y mayor será la información que podremos obtener para el descifrado, será mejo descifrar el quijote que una sola palabra.
 

Métodos criptográficos

Los métodos criptográficos deben ser una herramienta que permita transformar una información en otra nueva ( a ser posible ininteligible ), ya que esta nueva información pueda ser descifrada siempre que se le permita.
El mecanismo para establecer los métodos criptográficos deben contener una clave que es la que permitirá descifrar la información.
 

Criptosistema
Un criptosistema es una quíntupla formada por  cinco conjuntos ( M, C, K, E, D)

M: Conjunto de todos los posibles mensajes en claves. En principio infinitos.
C: Conjunto de todos los posibles mensajes cifrados.
K : Conjunto de todos los posibles claves.
E: Conjunto de todos los posibles transformaciones de cifrado.
D: Conjunto de todos los posibles transformaciones de descifrado.

Propiedad que debe cumplir un cierto sistema para que sea utilizable, es la única condición básica:

Ciframos m en c:
m pertenece a M
Ex (m) = c
Donde c pertenece a C

Desciframos c en m:

Dx ( c ) = m
 

Fundamentos teóricos para el diseño de algoritmos y su posible fortaleza.

2.1.1 Entropía
Concepto que introdujo Shannon (BELL laboratory) fórmula del libro matemáticas de la información.
En el que su concepto fundamental es la entropía. Ya introducido por físico en 1700.
Es la medida del orden, aparece en termodinámica, es una magnitud que no se conoce en su totalidad.

Principios de termodinámica:
· La energía ni se crea ni se destruye.
· El trabajo se puede transformar en energía, pero la energía no se puede transformar en trabajo sin perder energía.

Teoría de los gases: Estudiado el movimiento de las partículas en un gas, aparece una magnitud que se comporta igual que la entropía de la termodinámica, aunque esta relación no esta probada.

Entropía: Relación que existe entre desorden y uniformidad.

En la informática hay una entropía cuando surge una imprevisibilidad que irá relacionada con el desorden y la uniformidad.
 

· Cantidad de información
Imaginemos que tenemos una serie de sucesos, P(xi). Donde la probabilidad del suceso xi está comprendido en [0,1].
Mediante el algoritmo de la probabilidad tendremos un número menor que 1. Por lo que al aplicar el algoritmo tendremos un rango [¥,0].

Cantidad de información : -Cod P(xi)

Si a cada cantidad de información se le multiplica el peso de su probabilidad, obtendremos la entropía:

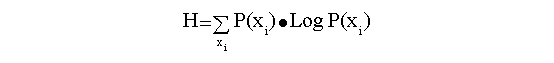
En un principio tomaremos un algoritmo en base 2.
 

Ejemplos:

Hallaremos la entropía para la probabilidad de que salga un 2 en un dado.

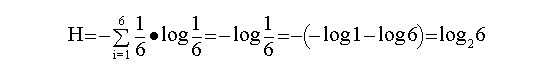
Donde el rango de H será: 0 <= H <=  log2 H
Por se la entropía máxima, podemos comprobar que esta entropía es máxima en un sistema en el que hay seis elementos posibles.
 

Hallaremos la entropía para la probabilidad de que salga una bola blanca en una caja en la que hay 49 bolas negras.

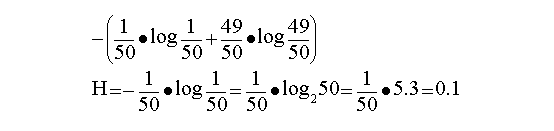
De lo que se desprende que cuanto más predecible es el sistema menor es la entropía.
 

Propiedades
Entropía máxima
En aquellos sucesos cuya probabilidad sea igual.

2.1.2 Redundancia
Indica la cantidad de información que está repetida. Esta información es sobrante.

D = R -r

Índice
El índice de la entropía mide la cantidad de bits que necesitamos para codificar cada uno de los mensajes en un lenguaje.

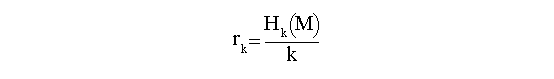
Donde:
M: Lenguaje
Hk (M): Es la entropía de mensajes con longitud k.

Fórmula para el índice absoluto(rk):

R = log2 (m)
 

2.2 Matemática discreta

Sistema probabilístico de 2 variables (Entropía de dos sistemas)

Probabilidad conjunta (Independiente): P(xi, yj)
Probabilidad condicionada(Dependiente): P(xi / yj)

Método de Valles:

Ley de la entropía total:

H(X,Y) = H(X) + H(Y)

H(X/Y) = H(X) + H(Y/X)

H(X/Y) <= H(X)

Si X e Y son independientes : H(X,Y) = H(X)
Cantidad de información que una variable tiene sobre otra:

I(X,Y) = H(X) – H(Y/X)

Cantidad de información que X contiene sobre Y.

Criptosistema seguro de Xanon o criptosistema ideal:

I(C,M) = 0

Es alcanzable de forma difícil, el hecho de conocer C no nos dice nada sobre M.
Para que un sistema cumpla esto es necesario que el cardinal de las clases sea igual al cardinal de los mensajes.
En la práctica es casi imposible de manejar, es decir no es manejable. Sólo será manejable en situaciones concretas.
El conjunto de mensajes (M) no es excesivamente grande.

Concepto de información
Se representa de la siguiente forma: H(M/C)
Sistema segundo de Xanon: H(M) = H(M/C)

Distancia de unicidad
Longitud máxima de lenguaje cifrado que lleva H(K/C) hacia cero. La cantidad de mensaje cifrado necesario para describir la clave.
Lo ideal es que sea ¥, es decir, aunque tengamos todo el texto no podamos descifrar la clave.
 

Técnicas para ocultar redundancia
Confusión
Intenta ocultar la relación (k) existente entre el mensaje (M) cifrado y el texto real (C).
El mecanismo más simple es la sustitución: Sustituir un símbolo del texto plano por otro
Difusión
Diluir la redundancia del texto por todo el texto cifrado, se consigue por transposición, es decir, en cambiar las cosas de su sitio.
 

2.3 Problemas computacionales

Aritmética modular
Es la aritmética que trabaja con conjuntos de números restringidos a un conjunto limitado.
Donde n dará a entender el módulo (número máximo prefijado)

Donde a, b, n pertenece a N
Siendo a congruente en b (mod n) Si a = b + kn

Lo números que existen estarán entre 0 y n-1 es decir [0, n-1].

Concepto del máximo común divisor
Nos basaremos en el algoritmo de Euclides.
Dadas a, b
Si m/a y si m/b, entonces m/(a – kb)
m/(a – kb) º m/(a mod(b))
Donde si definimos (a mod(b)) = c
Obtenemos m/(b mod c)

Ejemplo:
Tenemos
g₀ = a
g₁ = b
mientras (g₁ <> 0)
{
 x = g₀ % g₁
 g₀ = g₁
 g₁ = x
}
go

Concepto de inversas
Si m.c.d.(a, n) = 1, implica que a tiene inversa en módulo n.
Cabe destacar que a y n serán números primos entre sí por no compartir ningún divisor.

Existe a^-1 / a · a^-1  =  1      (mod n)

Conjunto de residuos
Denominaremos el conjunto de residuos en mod n al conjunto:
CR = {1, 2, 3, ..., n-1}

Conjunto de residuos en módulo m, los números que son primos entre sí.
CRR = {1, 5, 7, 11} con respecto a m = 12
Card(12) = 4

El cardinal de CRR se denomina en función de Euler

Donde p_i representa los números primos.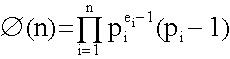
Y e_i es el número de veces que aparecen repetidos.

Ejemplo
Dado el número 12, hallar su cardinalidad.
12 = 31 · 22
f(12) = 30 · 2 · 2 · 1 = 2 · 2 = 4

Para utilizar el método de Euler se debe conocer al factorización en números primos para conocer el cardinal f(n).

Teorema de Fermat
El teorema de Fermat indica si un número no es primo, y si el número es primo indica que tiene probabilidad de serlo pero no lo asegura.

Si m.c.d.(a, n) = 1
        a^f(n) = 1     (mod n)
Si p es primo entonces a^p-1 = 1

a^f(n) = a · a^f(n)-1 = 1

Donde:  a^-1 = a^f(n)-1
Si n y a son primos y conocemos f(n).
Lo difícil de un número es calcular f(n).

La exponenciación rápida
Calcularemos a^b.
Usamos el algoritmo de la exponenciación rápida.
a^b
b = 2⁰b₀ +  2¹b₁ + … + 2ⁿb_n
Traducción binaria: b_0...n son 0, 1(bits)
 

Y su correspondiente algoritmo es:
Exprapida(a,b)
{
 Z = b
 X = a
 R = 1
 Mientras ( z ³ 0 )
  {
   si z % 2 = 1 entonces r = r * x
   x = x + x
   z = z/2
  }
}

Método de Lemans
Método válido para la saber si un número NO es primo, para saber con certeza si un número es primo deberemos aplicar repetidamente el test de Lemans. Queremos saber si un número es primo, para ello elegiremos un número menor que el número que queramos conocer si es o no primo y se le aplicará el test.

Queremos saber si p es primo.
Cogemos un número a, donde a < p y se le aplica el test.
 

SI b <> 1 Y b <> p-1 entonces p NO es primo
SINO 50% de probabilidades de que p sea primo y volveríamos a repetir el test con otro número para una mayor fiabilidad.

Pararíamos al repetir el test x veces, a una mayor repetición del test tendremos una mayor probabilidad de que el número sea primo y por lo tanto una mayor fiabilidad.

¿Cómo generar un número primo gordo?
Generamos un número aleatorio gordo, con el número de bits que queramos y en su número binario le añadimos un 1 al principio. Lo dividiremos entre los primos entre 2000 y 1. Tenemos una probabilidad muy alta de que sea primo, luego de aplicarlo al método de Lemans.

Números primos fuertes
Se definen primos fuertes cuando cumplen:
Siendo p, q dos números primos.

1: m.c.d.[(p-1), (q-1)] es pequeño
2: p-1 y q-1 tienen algún factor primo grande, llamemosle (p´, q´)
3: p´-1 y q´-1 tienen algún factor primo grande
4: p´+1 y q´+1 tienen algún factor primo grande

Estas son medidas anti-criptoanálisis.
Queremos un número n donde n=p·q, y de esta forma n no se puede factorizar.

Generar números aleatorios
Un número es aleatorio si es infinitamente impredecible.
Un ejemplo sería utilizar el micro de una tarjeta de sonido y el número de la tarjeta será aleatorio.

Generar una secuencia de números aleatorios.
Se utiliza una fórmula que dado un número aleatorio inicial, genere una secuencia de números aleatorios, y en el caso de que cambiemos el número inicial cambie toda la secuencia.

Ejemplo: La función randomize, utilizada con el la hora del sistema genera números aleatorios ya que la hora se refresca muy rápidamente y no da pie a repetir un número, respetando por lo tanto la aletoriedad que se busca.

Randomize (time())
 

2.4 Algoritmos de cifrado clásico

Cifrado por sustitución
Un ejemplo simple y claro de algoritmo de sustitución el método de cifrado César, el cual es un tipo de cifrado monoalfabético. Su forma de utilización es la de utilizar dos alfabetos, la forma de implementar los alfabetos será:

Elegiremos un primer alfabeto posteriormente escribiremos un segundo alfabeto basándonos en un una clave(un número). El segundo alfabeto resultará de desplazar a cada componente del alfabeto primero tantas posiciones como nos indique la clave.

Ejemplo:
Alfabeto primero:
A B C D E F G H I J K ... T U V W X Y Z

Clave: 3

Alfabeto segundo:
D E F G H I J K L M N ... W X Y Z A B C

En este método para cifrar un mensaje primero elegiríamos la clave para poder realizar el segundo alfabeto. De esta forma obtenemos dos alfabetos y tenemos la posibilidad de cifrar y descifrar.

Cifrado: Miramos el alfabeto primero y escribiremos los caracteres del alfabeto segundo.

Descifrado: Miraremos el alfabeto segundo y escribiremos los caracteres del alfabeto primero.

Ejemplo:
El mensaje a cifrar será: HOLA
Utilizaremos clave = 3, el resultado será:
Mensaje cifrado: KRDO
 

Cifrador polialfabético de Vigenere
En este tipo de cifrado contamos con varios alfabetos, tendremos tantos alfabetos como indique la clave.
Nos basaremos en un alfabeto principal del que se derivarán los alfabetos secundarios, estos alfabetos secundarios se desplazarán del alfabeto principal tantas veces como indique la clave.

Ejemplo:
Alfabeto principal:
A B C D E F G H I J …

Clave: Clave(3, 6, 2)
De la cual se desprende que tendremos 3 alfabetos secundarios.

Clave 3:
D E F G H I J K L M

Clave 6:
G H I J K L M N O P

Clave 2:
C D E F G H I J K L

Las funciones de cifrado y descifrado e realizan de la siguiente forma:
Cifrado
Seleccionaremos el mensaje original e iremos cogiendo caracteres que los cambiaremos por los caracteres que se encuentren en los alfabetos secundarios según indique la clave. Si hemos finalizado de leer las claves y aún quedan caracteres por cifrar volveremos al primer valor de la clave que nos indica que alfabeto utilizar.

Descifrado
El paso contrario al cifrado.

Ejemplo:

Mensaje a cifrar: AFFF
Clave: clave(3,6,2)
Mensaje cifrado: DLGI

Cifrado mediante trasposición
En este tipo de cifrado no se efectúa ninguna sustitución de letras en el mensaje, sino que atendemos al contenido y a la posición del carácter en el mensaje.

Ejemplo:
Clave = {5, 6, 1, 2, 4, 3}

Mensaje original: Hola_c
Mensaje cifrado: lac_Ho

Como se puede observar la clave indica la nueva posición que ocupará el carácter del mensaje original en el mensaje cifrado. Para descifrar el mensaje se realiza el contrario del cifrado.

Nota
En el caso de cifrar mensajes y sobrar espacio, rellenaríamos ese espacio con caracteres aleatorios. Ya que de esta forma es más difícil que puedan hallar el método y la clave de descifrado.
 

2.5 Criptografía actual

De los objetivos del tema 1, hay una herramienta que ayuda concretamente a la confidencialidad, esta herramienta es la criptología. La criptología se puede descomponer en dos campos que son el campo de la criptografía y el campo del criptoanálisis.

La criptografía es el “arte” de ocultar la información, es una ciencias de carácter histórico. Consiste en una serie de métodos que transforman la información en otra información que no permite su comprensión.

El criptoanálisis esta formado por una serie de técnicas que intentan descifrar una información encriptada de una forma no lícita ( desde el punto de vista técnico).

El criptoanálisis desde un punto de vista legal puede ser correcto o no, dependerá de cómo haya sido cifrado y de la información adicional de la que dispongamos en ese momento.

Siempre será mejor trabajar con secuencias largas de criptografía, ya que a una mayor cantidad de información mayor será la cantidad de cifrado y mayor será la información que podremos obtener para el descifrado, será mejo descifrar el quijote que una sola palabra.
 

2.5.1 Criptografía de clave privada (DES, IDEA, RC4).

Estos criptosistemas son los más sencillos y los más antiguos.
Los criptosistemas de clave privada se caracterizan por utilizar para el cifrado y descifrado la misma clave, la cual se mantiene secreta. Como usamos la misma clave secreta para cifrar que para descifrar se denominan “simétricos”, en contraposición a los de clave pública denominados asimétricos.
 

El algoritmo DES

El NIST desarrolló el algoritmo DES (Data Encription Estándar), un algoritmo de clave simétrica que ha estado en vigor durante muchos años. Aunque a sido declarado oficialmente “muerto” hace 5 o 6 años, debido a que varias empresas se dedicaban a descifrar información a terceros y porque se quedó “corto” con los ordenadores actuales.

En vista del fracaso de la NSA y el NIST se decidió abrir un concurso para hallar un algoritmo y estandarizarlo como método.

El algoritmo en síntesis, cifra un bloque de 64 bits de texto en claro en un bloque de 64 bits de texto cifrado. Para ello usa una clave externa de 64 bits en los que los bits de las posiciones octavas de cada octeto son bits de paridad impar.
El algoritmo consta de 16 iteraciones. En cada una de ellas se usan las operaciones de “Ô exclusivo”, permutaciones y sustituciones. Las permutaciones son de tres tipos: permutaciones simples, permutaciones expandidas (se duplican ciertos bits) y permutaciones restringidas (se eliminan ciertos bits).
Las sustituciones se refieren a sustituciones no lineales que se expresan en las tablas de las denominadas cajas.

El algoritmo DES sirve tanto para cifrar como descifrar la información.
Detalle del algoritmo DES:
 

El algoritmo DES efectúa las siguientes operaciones:

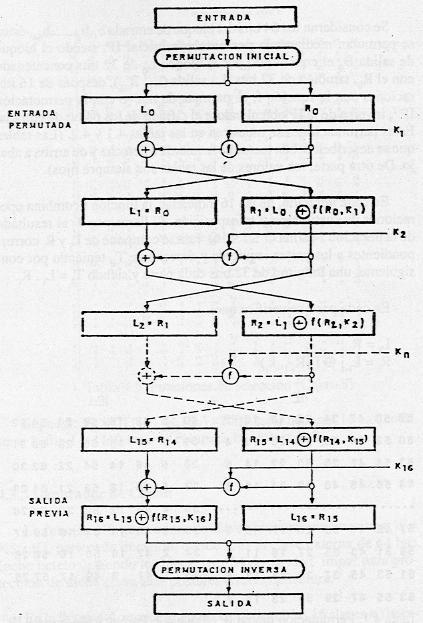
Se consideran los 64 bits del bloque de entrada, éstos se permutan mediante permutación inicial IP, siendo el bloque de salida B0 el constituido por el bloque l0 de 32 bits concatenado con el r0, también de 32 bits. La salida (L16 R16), después de 16 iteraciones con la función f, se permuta de nuevo con la permutación inversa de IP, obteniéndose el cifrado de los 64 bits de entrada.

En cada iteración, de las 16 indicadas, la función f combina operaciones de sustitución y transposición.
Si llamamos Ti al resultado de la iteración i-ésima (1£i£16) ésta se compone de Li y Ri correspondientes a las partes izquierda y derecha de Ti, teniendo por consiguiente, una longitud de 32 bits cada parte y siendo Ti = Li · Ri.
En cada paso se verifica que:

Li = Ri-1
Ri = Li-1 Ô f(Ri-1, ki)

Donde ki-1 es una clave de 48 bits generadora de claves ki=KS(i, k) siendo K la clave externa de 64 bits.
En el último paso las partes del resultado de L y R no se permutarán, y en su lugar se concatenan como R16 · L16 que se toman como entrada a la permutación IP-1. Esto es necesario para que el algoritmo sirva tanto para el cifrado como para el descifrado.

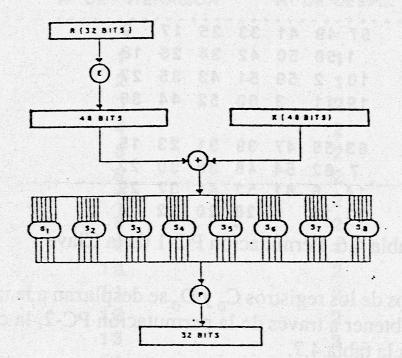
La función de cifrado f(R, ki) tiene como entradas los 32 bits correspondientes a la mitad derecha de la iteración anterior (Ri-1) y lo 48 bits de la clave ki. La cadena de bits de Ri-1 se expande a 48 bits mediante la tabla E de expansión de bits donde permutan los 32 bits y alguno de ellos se duplican.

La salida de 48 bits de la expansión de Ri-1  y ki se suman “O exclusivo” y la salida se reparte en 8 bloques de 6 bits cada uno.
 

E(R_i-1) Ô ki = B1 · B2 · B3 · B4 · B5 · B6 · B7 · B8

Cada bloque Bj, de 6 bits sirve como entrada a cada una de las 8 cajas Sj. Estas cajas implican una transformación no lineal que da como salida una secuencia de 4 bits para una entrada de 6 bits, Sj(Bj). Estas salidas se concatenan dando lugar a 32 bits, que se someten a al permutación P. Al final la salida de la función f es igual a:
 

P(S1(B1) · S2(B2) · … · S7(B7) · S8(B8))

Las cajas S reciben una información de 6 bits, transformandola en 4 bits.

Para cambiar el algoritmo sólo se cambian las cajas, al cambiarlas el algoritmo cambia totalmente.

Esquema de la función f(R, ki):
 

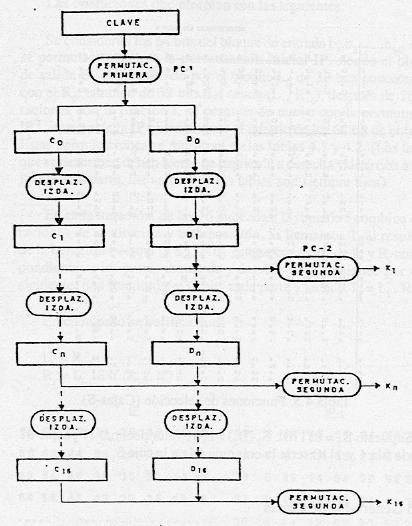
El algoritmo DES genera las claves mediante la función KS que proporciona una clave ki = KS(i, K), para cada iteración, donde K es la clave externa de 64 bits, siendo los bits 8, 16, ...64 de paridad impar para protección de dicha clave ante posibles errores de lectura.

En el sigiente esquema se muestra como se obtinen las 16 claves ki (internas):
 

Los 64 bits de la clave K se permutan según la permutación PC-1, que sin tomar los bits de paridad permuta los 56 bits restantes, dejando la salida en los registros C₀ y D₀.
Los contenidos de los registros C₀ y D₀ se desplazan a la izquierda una vez para obtener a través de la permutación PC-2 la clave ki.

Las sucesivas claves internas se obtienen a partir de los registros Ci y Di obtenidos después de realizar los sucesivos desplazamientos a izquierdas de los contenidos de los registros C y D, de forma que:
 

Ci = LSi(Ci-1)
Di = LSi(Di-1)

Donde LSi es un desplazamiento circular a la izquierda en un número de posiciones dependiendo de la iteración de que se trate.

La clave interna ki = PC-2 (Ci · Di)

El descifrado se realiza utilizando el mismo algoritmo descrito, si bien en la primera iteración se utiliza la clave interna k16, la k15 en la segunda y así sucesivamente, hasta la k1 que se emplea la iteración 16. Esto se hace así, ya que la permutación final IP-1 es la inversa de la permutación inicial IP, y por otra parte:
 

Ri-1 = Li
Li-1 = Ri Ô f(Li, Ki)

Así pues, se invierte el orden de las claves, pero el algoritmo no se invierte.

Hay que tener en cuenta que existen algoritmos que al aplicarlo contienen puntos flacos, en el DES al aplicar las 16 iteraciones ya no se puede descifrar, es decir no contiene puntos flacos.
 

El algoritmo IDEA

Debido a la previsible retirada de DES, prestigiosos criptógrafos de todo el mundo han estado trabajando desde los últimos años de la década de los ochenta para encontrar algoritmos, de un lado compatibles con DES (debido al gran número de productos basados en DES utilizados en todo el mundo), y de otro, lo suficientemente robustos como para sustituirle con garantías.
IDEA (International Data Encryption Algorithm) fue desarrollado en Suiza por Xuejia Lai y James Massey en 1992. Se trata de un algoritmo iterativo que trabaja sobre bloques de 64 bits utilizando claves de 128 bits, usando el mismo algoritmo tanto para cifrar como para descifrar. El proceso de cifrado consta de ocho fases idénticas en la que lo único que varía es el sub-bloque de clave utilizado, terminando el cifrado con una transformación de la salida. En cada paso se utilizan tres operaciones: suma bit a bit, multiplicación bit a bit y OR exclusivo.

Se estima que IDEA es más seguro que DES, el algoritmo IDEA es bastante seguro, y hasta ahora se ha mostrado resistente a multitud de ataques. Una característica del agoritmo es que no presenta claves débiles (En realidad, consta de un reducido subconjunto de claves que pueden dar ciertas ventajas a un criptoanalista, pero la probabilidad de encontrarnos con una de ellas es de 1 entre 2⁹⁶, por lo que no representan un peligro real.). Aunque, debido a su longitud de clave imposibilita en la práctica un ataque por la fuerza bruta.
Las bases teóricas y la implementación de los diferentes sistemas criptográficos que lo utilizan están sometidos a público escrutinio. Los programas actuales que implementan IDEA son tan rápidos como los que implementan DES.

IDEA se basa en los conceptos de confusión y difusión, haciendo uso de las siguientes operaciones elementales:

 - XOR.
 - Suma módulo 2¹⁶ .
 - Producto módulo 2¹⁶ + 1.

El algoritmo IDEA consta de ocho fases. Dividiremos el bloque X a codificar, de 64 bits, en cuatro partes X₁, X₂, X₃ y X₄ de 16 bits. Denominaremos Zi a cada una de las 52 subclaves de 16 bits que vamos a necesitar. Las operaciones que llevaremos a cabo en cada fase son las siguientes:

1 - Multiplicar X₁ por Z₁.
2 - Sumar X₂ con Z₂.
3 - Sumar X₃ con Z₃.
4 -  Multiplicar X₄ por Z₄.
5 - Hacer un XOR entre los resultados del paso 1 y el paso 3.
6 - Hacer un XOR entre los resultados del paso 2 y el paso 4.
7 - Multiplicar el resultado del paso 5 por Z₅.
8 - Sumar los resultados de los pasos 6 y 7.
9 - Multiplicar el resultado del paso 8 por Z₆.
10 - Sumar los resultados de los pasos 7 y 9.
11 - Hacer un XOR entre los resultados de los pasos 1 y 9.
12 - Hacer un XOR entre los resultados de los pasos 3 y 9.
13 - Hacer un XOR entre los resultados de los pasos 2 y 10.
14 - Hacer un XOR entre los resultados de los pasos 4 y 10.

La salida de cada iteración serán los cuatro sub-bloques obtenidos en los pasos 11, 12, 13 y 14, que serán la entrada del siguiente ciclo, en el que emplearemos las siguientes seis subclaves, hasta un total de 48. Al fi nal de todo intercambiaremos los dos bloques centrales (en realidad con eso deshacemos el intercambio que llevamos a cabo en los pasos 12 y 13).
Después de la octava iteración, se realiza la siguiente transformación:

1 - Multiplicar X₁ por Z₄₉.
2 - Sumar X₂ con Z₅₀.
3 - Sumar X₃ con Z₅₁.
4 - Multiplicar X₄ por Z₅₂.

Las primeras ocho subclaves se calculan dividiendo la clave de entrada en bloques de 16 bits. Las siguientes ocho se calculan rotando la clave de entrada 25 bits a la izquierda y volviendo a dividirla, y así sucesivamente.

Las subclaves necesarias para descifrar se obtienen cambiando de orden las Zi y calculando sus inversas para la suma o la multiplicación.
Puesto que 2¹⁶ + 1 es un número primo, nunca podremos obtener cero como producto de dos números, por lo que no necesitamos representar dicho valor. Cuando estemos calculando productos, utilizaremos el cero para expresar el número 2¹⁶ (un uno seguido de 16 ceros). Esta representación es coherente puesto que los registros que se emplean internamente en el algoritmo poseen únicamente 16 bits.
 

El algoritmo RC4

El algoritmo RC4 fué desarrollado por Ron Rivest, uno de los coautores del algoritmo RSA, en 1987.  Su implementación es extremadamente sencilla y rápida, y está orientado a generar secuencias en unidades de un byte, además de permitir claves de diferentes longitudes.Durante varios años, se ha tratado de algoritmos con propietario lo cual implica que no puede ser incluido en aplicaciones de tipo comercial sin pagar los royalties correspondientes,  y sus detalles no fueron hechos públicos. De este modo, su seguridad se basaba en el prestigio de su autor y en el respaldo que les daba RSA Data Security, Inc., para las que los desarrolló. Sin embargo, en 1994 RC4 fue sometido a ingeniería inversa y los resultados fueron publicados en los grupos de noticias de  Internet. Las pruebas hechas a dicho diseño se ajustan a los resultados esperados por lo que es razonable pensar que el diseño publicado es correcto.

RC4 consta de una longitud de clave variable. Sin embargo, se trata de un cifrador de flujo. Dicha descripción consta de una S-Caja de 8x8, que almacenará una permutación del conjunto {0,..., 255) . Dos contadores i y j se ponen a cero. Luego, cada byte Or de la secuencia se calcula como sigue:

1 - i = (i + 1) mod 256
2 - j = (j + S_i) mod 256
3 - Intercambiar los valores de S_i y S_j
4 - t = (S_i + S_j ) mod 256
5 - O_r = S_t

Para calcular los valores iniciales de la S-Caja, se hace lo siguiente:

1. S_i = i , Para cualquier i que: 0 <= i <= 255
2. Rellenar el array K₀ a K₂₅₅ repitiendo la clave tantas veces como sea necesario.
3. j = 0
4. Para i = 0 hasta 255 hacer:
            j = (j + S_i + K_i) mod 256
            Intercambiar S_i y S_j .

El algoritmo RC4 genera secuencias en las que los ciclos son bastante grandes, y es inmunea los criptoanálisis diferencial y lineal, si bien lgunos estudios indican que puede poseer claves débiles, y que es sensible a estudios analíticos del contenido de la S-Caja. De hecho, algunos afirman que en una de cada 256 claves posibles, los bytes que se generan tienen una fuerte correlación con un subconjunto de los bytes de la clave, lo cual es un comportamiento muy poco recomendable.

Como el resto de productos criptográficos desarrollados en EE.UU., las restricciones a su exportación son muy fuertes. RC4 tiene un estatus especial que facilita la concesión de licencias de exportación de productos basados en dicho algoritmo, pero limitando la longitud de su clave a 40 bits.
A pesar de las dudas que existen en la actualidad sobre su seguridad, es un algoritmo ampliamente utilizado en muchas aplicaciones de tipo comercial. el algoritmo RC4 se usa en centenares de productos comerciales. El protocolo SSL también los usa.
 

2.5.2 Criptografía de clave pública (RSA)

Los criptosistemas de clave pública constan de dos claves: una clave pública y una clave privada.
Se les suele llamar asimétricas por sus dos claves.
Lo normal es usar una clave para cifrar y otra para descifrar. Las claves deben ir a pares, es decir, dada una clave pública debe acompañarle una clave privada ( sólo una ) para poder descifrarlo.
Todo el mundo puede conocer la clave pública, pero NO la clave privada, por lo que todo el mundo puede cifrar pero no descifrar.
Recordemos que el objetivo del cifrado es la autenticidad.

Cada persona tiene sus dos claves, y al enviar un mail se envía con la clave pública de destino por lo que sólo el destino lo puede descifrar. Porque se la envía con su clave pública y sólo el destinatario tiene la clave privada.

Los sistemas de clave pública son muy difíciles de implementar, tienen un coste algorítmico y computacional muy grande por la gran cantidad de operaciones que se necesita el algoritmo. A mayor clave, mayor coste computacional.

Los sistemas de clave pública aparecen en 1976, oficialmente el primer algoritmo de clave pública es el de Rybest-Shair-Ackerman (RSA). Años después la NSA. NIST, una agencia de USA que buscaba la estandarización de técnicas de seguridad, a partir de esto a estandarizado una serie de algoritmos.
El RSA como empresa patentó el algoritmo hasta que hace algunos años, por lo que ahora se utiliza una serie de software de forma libre.

La seguridad del RSA radica básicamente en la dificultad computacional de la factorización de grandes números.
Esta probado que, actualmente no existe un algoritmo para factorizar un número de 200 dígitos en un tiempo razonable.

Los posibles procedimientos criptoanalíticos que se aplicar para vulnerar algoritmos son:

a) Factorización de n.
b) Calculo de §(n) sin factorizar n.
c) Determinar d sin factorizar n o calcular §(n).
d) Calcular la función D de alguna forma.
 

A continuación se exponen estos posibles procedimientos:

a) Factorización de n.
La factorización de n permite vulnerar el método ya que se puede obtener §(n) y fácimente d.
Por otra parte el algoritmo más rapido de factorización conocido debido a R. Schroeppel, factoriza un número n en:
 

Pasos

Si suponemos que un paso de este algoritmo en un ordenador llevará 1 microsegundo, el tiempo de factorización según Schroeppel sería:
 

Se recomienda utilizar n de longitud 200 dígitos, al objeto de proporcionar un alto grado de seguridad.
El método, en función de la longitud de n, proporciona diferentes niveles de seguridad que pueden ser convenientes en función del grado de secreto que se dé a la información a cifrar.
 

b) Calculo de §(n) sin factorizar n.
Si se obtiene §(n) se vulnera el sistema calculando d como número asociado de e (público) mod §(n) mediante el algoritmo de Euclides modificado.

Este procedimiento es equivalente a factorizar n, pues si se conoce §(n) se puede encontrar p y q.
Así, (p + q) se obtiene de n y §(n) = n - (p + q) + 1 y (p - q) = ((p + q)² - 4n)^1/2, por tanto:
 

q = ((p + q) - )p - q)) / 2 y p = n/q

y por lo tanto se vuloneraría el método.
 

c) Determinar d sin factorizar n o calcular §(n).
d debe elegirse entre un gran conjunto de números de forma que la búsqueda exhaustiva resulte no factible. Por otra parte, conocido d se puede factorizar n fácilmente, pues:

                        e.d - 1 = k . §(n)

y Miller ha demostrado como factorizar n conocido un múltiplo cualquiera de §(n).
Con ello se llega a la conclusión de que, si n es grande, no se puede determinar d de forma más fácil que factorizando n.
 
 

d) Calcular la función D de alguna forma.
Se piensa que M se podría obtener calculando la raíz e-esíma de C, según:
 

Pero se cree que este problema pertenece a la clase NP-completa según los autores del algoritmo.

Ejemplo de cifrado RSA
Supuesto que el corresponsal A quiere entrar en el sisteman entonces, elige los enteros primos p = 5 y q = 11 resultando n = p x q = 5 x 11 = 55.
Así, §(55) = 4 x 10 = 40. A continuación se selecciona la clave privada d = 23. Como el m.c.d. (e,23) = 1; se cumple 3 x 23 = 1 mod 40, obteniéndose e = 7, siendo e el inverso multiplicativo de 23 módulo 40.

Sea el mensaje "STOP" que se codifica numéicamente, como 20 21 16 17 y se cifra por bloques de letras, en este caso se hace letra a letra, así, para la "S"
 

C = M^e mod n = 20⁷ mod 55 = (((1)² x 20)² x 20)² x 20 mod 55 = 15

Utilizando el algoritmo de la exponenciación rápida que expresando en binario, en este caso, e = 7 = 111 permite la evaluación de la exponenciación de M.

Para el caso que se trata, al ser d = 23, en binario 10111, C se descifraría como:

M = C^d mod n = 15²³ mod 55 = (((((1)² x 15)²)² x 15)² x 15)² 15 mod 55 = 20
 

2.5.3 Software criptrográfico

Hay varios programas que se basan en encriptar/desncriptar. El más popular es probablemente el PGP que corresponde a pretty good privacy (privacidad bastante buena). PGP es un programa que te permite encriptar algo con la clave pública de los receptores a los que va destinado y desencriptar con la clave secreta si es que tú eres el receptor de un mensaje cifrado.
Encriptar usando algoritmos de clave pública tiene 2 inconvenientes:
Es un proceso lento: Elevar un número a otro y luego hacer el módulo n es un proceso lento, por tanto es mucho más rápido encriptar con métodos de clave simétrica.
Sólo un único destinatario podrá leer el mensaje: esdecir, sólo la persona que tiene la clave privada necesaria será capaz de leer el mensaje, así que si quieres enviar un mismo mensaje a varios amigos, tendrás que encriptarlo una vez para cada uno de tus amigos con su clave pública y enviar a cada uno el mensaje encriptado que son capaces de desencriptar.
Estos dos inconvenientes se pueden solucionar fácilmente, tal y como lo hace el PGP. En lugar de encriptar el mensaje con un algoritmo de clave pública, lo encripta con un algoritmo de clave simétrica usando como clave simétrica algo absolutamente aleatorio e impredecible. A continuación, encripta la clave simétrica que ha generado para encriptar usando las claves públicas de los destinatarios. El resultado es un mensaje encriptado con una clave que nadie conoce, seguido de esa clave, pero encriptada con la clave pública del destinatario. Si hay más de un destinatario, se añade la clave simétrica encriptada tantas veces como destinatarios haya, encriptandola cada vez con la clave pública de uno de los destinatarios del mensaje. Con esto, uno de los destinatarios del mensaje puede desencriptar la clave simétrica (una de las copias encriptadas que hay va destinada a él así que está encriptada con su clave pública) y con la clave simétrica puede desencriptar el mensaje completo. De esta forma conseguimos acelerar el proceso (encriptar con clave simétrica es muy rápido, y con clave pública sólo se encripta la clave simétrica que es algo muy corto), y además permitimos que varias personas puedan desencriptar el mismo mensaje cifrado (ya que la clave simétrica necesaria para desencriptar el mensaje está encriptada con la clave pública de cada receptor, y añadida al final del mensaje encriptado).
Así que un documento encriptado con PGP está formado por varias partes (mirar 2.6.1 Firma digital):

Parte 1:
Mensaje original encriptado con IDEA, usando una clave K generada aleatoriamente en el momento de encriptar el mensaje.

Parte 2:
K encriptada con la clave pública RSA del receptor 1.

Parte 3:
K encriptada con la clave pública RSA del receptor 2.
 

Ahora la seguridad del sistema no sólo depende de que no se pueda hayar la clave privada de alguno de los receptores del mensaje sino también de que no se pueda encontrar K. Para ello, el algorimto de clave simétrica que usemos ha de ser robusto y seguro, y lo que usa PGP 2.6.x (es decir, IDEA) lo es... al menos de momento. Y también ha de ser realmente impredecible la K, es decir, hemos de poder generar números realmente aleatorios para formar la clave K y que esos números no sean predecibles. Respecto a las claves públicas, existen métodos para factorizar un n de forma rápida, basados en propiedades matemáticas extrañas. De todas formas, aumentando el tamaño del número n se consigue hacer que estos métodos sean muy muy lentos. Por eso se recomiendan claves públicas en las que n sea un número de 512 bits, 768 bits, 1024 bits, o incluso 2048 bits si usas PGP 2.6.3i. Lo mejor es utilizar una clave de 2048 bits, ya que actualmente se han conseguido factorizar números de 129 digitos (512 bits aprox.) y se espera que pronto caigan los de 768 bits. En realidad, es posible que alguna agencia en USA ya sea capaz de factorizar 768 bits, ya que todas ellas invierten millones de dollares en investigación sobre estos temas cada año, y, al contrario que en las universidades, no comparten sus resultados con el resto del mundo. A nivel civil, se cree que se podrán factorizar números de 1024 bits en el 2004, y de 2048 bits en el 2014 si es que no se descubre nada nuevo que suponga una revolución en este campo... Es de suponer que los militares, la CIA, el FBI, etc... nos llevan ventaja, así que ponerse una clave de 2048 es bastante recomendable.
 

2.6 Estándares y aplicaciones criptográficas

2.6.1 Firmas digitales

Existen dos tipos de esquemas sobre firma digital, el que se denomina esquema de firma digital con apéndice y el esquema de firma digital con mensaje recuperable. También cualquier esquema de firma cuenta con dos partes la primera parte se denomina proceso de firma (similar al cifrado) y la segunda parte proceso de verificación de la firma (similar al descifrado).
El esquema más usado y conocido es el esquema de firma con apéndice. Algunos tipos de programas y como realizan el proceso de firmado.
Para crear la firma se utilizan funciones Hash y para su posible codificación se utilizan diversos métodos criptográficos.

Firma digital en el SMIME

Se utilizan los mensajes signed-dat, el proceso el el siguiente:
 

1 - Se calcula un resumen del contenido mediante una función Hash. Si hay varios firmantes con diferetnes funciones Hasa se calcula un resumen para cada algortimo.

2 - El resumen se encripta para cada firmante usando su clave privada.

3 - Se añade al contenido las firmas, los certificado y, si es necesario, las CRLs (listas de revocación de certificados).

Las funciones Hash utilizadas son SHA-1 y MD5, y los algoritmos de encriptación son DAS y RSA.
 

Firma digital en el PGP

En origen, el mensaje o fichero que queremos proteger va pasando por diferentes bloques que lo van transformando:

1 - Compresión
Utilizando el algoritmo pkzip.

2 - Firma digital
Se crea una firma digital del mensaje, utilizando la función de hash MD5. Dicha firma es cifrada con la clave privada del remitente usando el algoritmo RSA y añadida al mensaje. El usuario puede elegir la longitud de la clave asimétrica, y por tanto su grado de seguridad. Ahora bien, cuanto más larga sea la clave, más lento será el proceso.
cifrado.

3 - El cifrado
Se hace usando IDEA (criptografía de clave simétrica). La clave simétrica es generada aleatoriamente y transmitida al destinatario cifrada con su clave pública (algoritmo RSA de nuevo).

4 - Compatibilización con el protocolo de transmisión de correo electrónico.

5 - Segmentación.

En la recepción se realiza el proceso inverso, con lo que se obtiene el mensaje original, asegurando los requerimientos buscados.
 

2.6.1.1 Funciones Hash

Las funciones Hash pertnecen a la criptografía de clave simétrica. Son utilizadas principalmente para confirmar la integridad de los mensajes, así como su autenticidad. Las  funciones Hash son también usadas en la firma digital (ver 2.6.1). Como los documentos a firmar son en general demasiado grandes, mediante la función Hash asociamos una cadena de longitud 160 bits que los hace más manejables para el propósito de firma digital, transformando un mensaje de longitud arbitraria en un mensaje de longitud constante.

Para ello la función Hash toma como entrada una cadena de longitud arbitraria, digamos 5259 bits, luego divide éste mensaje en partes iguales, digamos de 160bits; como en este caso y en general el mensaje original no será un múltiplo de 160, entonces para completar un número entero de partes de 160 bits al último se le agrega un relleno, digamos de puros ceros. En nuestro caso en 5259 caben 32 partes de 160
bits y sobran 139, entonces se agregarán 21 ceros más.

Entonces el mensaje toma la forma X = X1, X2, X3,…,Xt donde cada Xi tiene igual longitud (160bits por ejemplo).
Posteriormente se asocia un valor constante a un vector inicial IV y

H0=IV

Ahora se obtiene H1 que es el resultado de combinar H0 con X1 usando una función de compresión f

H1 = f(H0,X1)

Posteriormente se obtiene H2, combinando H1 y X2 con f

H2 = f(H1,X2)

Se hace lo mismo para obtener H3

H3 = f(H2,X3)

Hasta llegar a Ht

Ht = f(Ht-1, Xt)

Entonces el valor Hash será:

h(M) = Ht

Basicamente lo que las funciones Hash realizan es tomar el mensaje partirlo en pedazos de longitud constante y combinar de alguna forma pedazo por pedazo hasta obtener un solo mensaje de longitud fija.

Las funciones Hash pueden operar como: MDC (Modification Detection Codes) ó MAC (Massage Authentication Codes).
Los MDC sirven para resolver el problema de la integridad de la información, al mensaje se le aplica un MDC (una función Hash) y se manda junto con el propio mensaje, al recibirlo el receptor aplica la función Hash al mensaje y comprueba que sea igual al Hash que se envió antes, entonces se acepta que el mensaje se a transmitido sin alteración.

Los MAC sirven para autenticar el origen de los mensaje así como también su integridad, para hacer esto se combina el mensaje M con una clave privada K y se les aplica un hash h(M,K). Se envía esto y al llegar a su destino si se comprueba la integridad de la clave privada K, entonces se demuestra que el único origen del mensaje es el que tiene la parte propietaria de la otra clave K.

Propiedades de las funciones Hash son:

1 - Resistencia a la preimagen
Significa que dada cualquier imagen, es computacionalmente imposible encontrar un mensaje x tal que h(x) = y, es decir, que h sea de un solo sentido.

2 - Resistencia a una 2° preimagen
Significa que dado x, es computacionalmente imposible encontrar una x’ tal que h(x) = h(x’), es decir, que h sea resistente a una colisión suave.

3 - Resistencia a colisión (fuerte)
Significa que es computacionalmente imposible encontrar dos diferentes mensajes x, x’ tal que h(x) = h(x’).

Las funciones hash más conocidas son las que se crean a partir de un block cipher como: DES.
Actualmente se ha podido encontrar debilidades en las funciones hash que tienen como salida una cadena de 128 bits, por lo que se ha recomendado usar salidas de 160bits.
 

2.6.1.2 Firma con clave pública

Proceso de firma aplicado al algoritmo RSA sobre el esquema de firma con apéndice, consiste en los siguientes puntos:

Proceso de Firma

1 - El mensaje a firmar es M, se le aplica una función hash que reduce su longitud de forma única a un mensaje H(M) de longitud de 128 o 160 bits, lo que permite ver cualquier mensaje de cualquier longitud como una cadena de caracteres de longitud constante.

2 -  H(M) se somete también a un proceso de codificación, por lo tanto se obtiene un número h(M), al que se le aplica la formula con la potencia d, equivalentemente con la clave privada del firmante para obtener

s = h(M)^d mod n

3 - Se envía entonces el mensaje firmado s

Proceso de Verificación

1 - El que recibe s, se supone conoce el mensaje M, aplica la función de verificación que depende de la clave pública de quien se dice propietario del
mensaje.

h' = s^e mod n

2 - Ahora se aplica la función hash al mensaje M y si h(M) = h’ entonces acepta la firma.
En un esquema con mensaje recuperable no es necesario saber el mensaje, después de que la firma es aceptada el mensaje puede recuperarse a partir de la firma.

Ejemplo:
Sean los parámetros p = 3, q = 5, fi = 8, m = 2, e = 3, d = 3.

Proceso de Firma
1 - La firma del documento m es: s = m^d mod n = 2³ mod 15 =8
2 - El mensaje firmado es entonces (m,s) = (2,8)

Proceso de verificación
3 - Aplicando la función de verificación s^e mod n = 8³ mod 15 = 2
4 - Como 2 (el obtenido de la anterior fórmula) = 2 (el mensaje enviado)
5 - Entonces la firma es válida
 

2.6.2 Infraestructuras de clave pública (PKI)

PKI (Public Key Infraestructure) que significa Infraestructura de Clave Pública. El PKI es el conjunto de protocolos, servicios y normas en los que se basa toda aplicación en criptografía de clave pública. La definición de PKI no está totalmente definida, por lo que consideraremos que una PKI incluye los servicios y protocolos necesario para la administración de claves, generalmente usando Autoridades de Certificación  y Autoridades de Registro, sin considerar la ejecución de operaciones criptográficas con las claves.
Servicios que generalmente proporciona una PKI están los siguientes:

- Registro de claves
Emisión de certificados correspondientes a una clave pública.

- Revocación de certificados
Cancelación de un certificado emitido previamente.

- Selección de claves
Obtención de la clave pública de un usuario.

- Evaluación de confianza
Determinación de la validez de un certificado y de las operaciones que autoriza.

- Recuperación y custodia de claves
Se ha sugerido que una PKI pueda ocuparse de estas cuestiones.
 

2.6.2.1 Certificación x509

El protocolo X.509 es el sistema de certificado de clave pública más utilizado, su utilidad es demostrar que una clave pública pertenece a
un usuario concreto. Su origen es el directorio X.500, inventado por la UIT para dar servicio al correo electrónico X.400. Actualmente se utiliza en los protocolos seguros y en los sistemas de correo Internet más conocido, excepto en el PGP. Permite trabajar con autoridad certificadora y anidar certificados para crear estructuras jerárquicas.

El estándar X.509 sólo define la sintaxis de los certificados, por lo que no está atado a ningún algoritmo en particular, y contempla los siguientes campos:

- Versión
La versión de protocolo X.509.

- Número de serie (Serial number)
Identificador único del certificado, asignado por la autoridad certificadora.

- Algoritmo de la firma del certificado (Signature)
X.509 permite utilizar diferentes algoritmos para firmar el certificado, este campo lleva el identificador del algoritmo.

- Autoridad de certificación (Issuer)
Nombre de la autoridad certificadora.

- Fechas de inicio y final (Validity)
El certificado sólo tiene validez entre estas dos fechas. Es conveniente no permitir un periodo de validez largo y a sí obligar a renovar certificado y claves con asiduidad.

- Usuario (Subject)
Nombre del usuario.

- Clave pública (SubjectPublicInfo)
La clave pública del usuario, permite múltiples longitudes.

- Identificador único de la autoridad certificadora (IssuerUniqueID)
Cada autoridad certificadora tiene un número de identificación único en el mundo.

- Identificador único del usuario (SubjectUniqueID)
Los usuarios tiene un identificador único en la autoridad certificadora para todos sus certificados.

- Extensiones
Posibles extensiones de la información.

- Firma de la autoridad certificadora
La autoridad certificadora firma con su clave privada todos los campos anteriores.
 

2.6.2.2 Las autoridades certificadoras

Las autoridades certificadoras surgen para solucionar una serie de problemas en la autentificació e integridad de los mensajes que circulan en Internet. Las autoridades certificadoras generan claves públicas y certificados para los usuarios que lo solicitan, además de dar a conocer sus claves públicas para las comprovaciones. Los usuarios se deben identificar personalmente para pedir un certificado a una autoridad certificadora. Para que en las autoridades certificadoras no se sufra una centralización se basan en una estructura jerárquica a nivel mundial. Las autoridades certificadoras locales son certificadas por otras de nivel superior hasta llegar a la principal que es de confianza en todo el mundo. Así se consigue que la confianza sea mundial y que la gestión pueda ser local para los procesos judiciales y facilitar el proceso de identificación personal.

Las autoridades certificadoras de orden superior certifican a las inferiores y se pueden anidar certificados desde las autoridades certificadoras principales hasta la clave del usuario. Esto permite comunicar de manera segura a dos usuarios, con la condición de que conozca la clave pública de la autoridad certificadora principal que obtendrá de su autoridade certificadora local.
 

2.6.2.3 Estándares RSA

La compañia RSA Data Security, Inc. realizó un intento de proporcionar unos estándares en criptografía de clave pública, que dió lugar a los PKCS (Estándares Criptográficos de Clave Pública). Estos estándares , los PKCS, no son estándares internacionales, es decir estándares totalmente válidos, aunque muchas empresas han participado en el desarrollo de estos estándares y son utilizdos por sus productos, la compañia RSA Data Security, Inc. se reserva la última palabra en su promulgación y revisión.
En la actualidad se trata de diez normas:

- PKCS#1 (RSA Encryption Standard)
Describe un método para la utilización del algoritmo RSA, reuniendo reglas que hay que tener en cuenta para que una implementación primero sea inmune a los diferentes ataques a que puede ser objeto, y por otro lado a que las diferentes implementaciones de RSA sean compatibles. Su propósito es producir firmas digitales de mensajes y mensajes cifrados utilizando la sintaxis definida en el estándar PKCS#7. Las firmas digitales se producen aplicando una función de hash al mensaje y cifrando la huella digital resultante con la clave privada del firmante. El mensaje y su firma digital se representan tal como indica PKCS#7. Para conseguir los envoltorios digitales, el mensaje se cifra primero con una clave simétrica y, después, se cifra dicha clave con la clave pública del destinatario del mensaje. Ambos componentes (sobre y clave cifrada) se representan juntos según PKCS#7. También describe una sintaxis, idéntica a X.509 para las claves públicas y privadas y tres algoritmos de firmado digital (MD2 y RSA, MD4 y RSA y MD5 y RSA).

- PKCS#2
 Incorporadas a PKCS#1.

- PKCS#3 (Diffie-Hellman Key-Agreement Standard)
Describe un método para implementar el intercambio de claves Diffie-Hellman, ya en desuso.

-  PKCS#4
 Incorporadas a PKCS#1.

- PKCS#5 (Password-Based Encryption Standard)
Describe un método para cifrar mensajes con una clave secreta (password) derivada de una frase de paso. Su objetivo primario es permitir la transmisión cifrada de claves privadas entre dos ordenadores, como se describe en el PKCS#8, aunque puede ser usada para cifrar mensajes. Emplea MD2 o MD5 para producir una clave a partir de una frase de paso. Esta clave se utiliza para cifrar con DES (en modo CBC) el mensaje en cuestión.

- PKCS#6 (Extended-Certificate Syntax Standard)
Describe una sintaxis para "certificados extendidos", entendiendo por tales un superconjunto de X.509, de modo que se pueden extraer certificados X.509 de estos certificados. Se incluyen atributos adicionales como puede ser la dirección electrónica. Una lista no exhaustiva de tales atributos se define en PKCS#9.

- PKSC#7 (Cryptographic Message Syntax Standard)
Es una sintaxis general para datos que pueden tener alguna operación criptográfica asociada, ya sea cifrado ("envoltorios digitales") o firmado (firmas digitales). La sintaxis es recursiva, de modo que se pueden anidar envoltorios digitales o cifrar datos cifrados previamente. También se permiten atributos adicionales, como marcas temporales (time stamps)... Una forma límite de utilización de esta sintaxis proporciona un método para distribuir certificados o listas de revocación de certificados. En este sentido, PKCS#7 es compatible con varias arquitecturas de gestión de claves basadas en certificados.

- PKCS#8 (Private-Key Information Syntax Standard)
Describe una sintaxis para la información de la clave privada, la cual incluye una clave privada y una serie de atributos, y una sintaxis para claves privadas cifradas (un algoritmo de cifrado basado en palabras de paso, como el descrito en el PKCS#5, podría ser usado para cifrar la información de clave privada). Una lista parcial de atributos puede encontrarse en PKCS#9.

- PKCS#9 (Selected Attribute Types)
Define algunos atributos para su uso en los certificados extendidos del PKCS#6, los mensajes firmados digitalmente de PKCS#7, la información de clave privada de PKCS#8 y para las peticiones de firmado de certificados definidas en PKCS#10.

- PKCS#10 (Certification Request Syntax Standard)
Describe una sintaxis para las peticiones de certificados. Una petición de certificados consiste en un nombre distinguido (distinguished name), una clave pública y una serie de atributos opcionales (parcialmente definidas en PKCS#9), todo ello firmado colectivamente con la clave privada de la persona que hace la petición. Las peticiones se envía a una Autoridad de Certificación, la cual transforma la petición en un certificado X.509 v.3 o en un certificado extendido (PKCS#6). Las autoridades de certificación pueden precisar procedimientos de petición no electrónicos y responder no electrónicamente. Estos procedimientos son específicos de cada autoridad y están fuera del estándar.

- PKCS#11 (Cryptographic Token Interface Standard)
Especifica una interfaz de programación llamada Cryptoki para su uso con dispositivos criptográficos de cualquier tipo (conocidos como tokens, tarjetas generalmente). Cryptoki tiene un enfoque basado en objetos permitiendo que aplicaciones realicen operaciones criptográficas sin conocer los detalles de la tecnología de los dispositivos. También define conjuntos de algoritmos que el token puede soportar.

- PKCS#12 (Personal Information Exchange Syntax Standard)
Describe la sintaxis para almacenar en software las claves públicas de un usuario, proteger sus claves privadas, certificados y cualquier otra información de relevancia criptográfica. Su propósito es permitir el uso de un único fichero de claves accesible por cualquier aplicación.

- PKCS#13 (Elliptic Curve Cryptography Standard)
Describe, de modo similar a como lo hace PKCS#1, un método para la utilización de algoritmos de curva elíptica. Describe la generación y validación de parámetros, la generación y validación de claves, el procedimiento de firmado y de cifrado...

- PKCS#15 (Smart Card File Format)
Este PKCS, aún en borrador, surge para cubrir ciertos aspectos no contemplados por PKCS#11. Para ello, trata de uniformizar la estructura de directorios y ficheros de las tarjetas inteligentes, el contenido de ciertos ficheros (como el de certificados) y el modo de acceder a ellos, de modo que se asegure la interoperabilidad entre aplicaciones, de modo que no dependan de la tarjeta instalada.