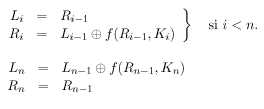[Indice][Tema
1] [Tema 2] [Tema 3] [Tema
4] [Tema 5]
Tema 2: Fundamentos
matemáticos de la criptología.
Dentro de la criptología hay dos partes:
-
Criptoanálisis: son las técnicas para descifrar la
información criptografiada.
-
Criptografía: es "el arte" de ocultar la información.
Se basa en unos métodos mediante los cuales su significado permanece
oculto a ojos ajenos.
Un método criptográfico debe permitir
convertir cualquier información en otra inentendible y se pueda
convertir cuando se tenga la autorización requerida (la clave).
Se denomina criptosistema a una quíntupla
formada por cinco conjuntos:
M ð conjunto
de los posibles mensajes en claro (sin cifrar). Este puede ser finito o
infinito.
C ð conjunto de todos
los mensajes cifrados.
K ð conjunto de todas
las claves.
E ð conjunto de transformaciones
de cifrado.
D ð conjunto de transformaciones
de descifrado.
La propiedad que debe cumplir un criptosistema:
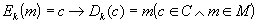 Esto quiere decir que cualquier mensaje cifrado puede ser descifrado conociendo
la clave.
Esto quiere decir que cualquier mensaje cifrado puede ser descifrado conociendo
la clave.
Hay dos tipos de criptosistemas los de clave
pública y los de clave privada.
Los de clave privada (o simétrico)
son los más antiguos y se caracterizan en que solo existe una clave
en el proceso de cifrar y descifrar que es privada y solo puede cifrar
y descifrar el contenido el poseedor de dicha clave.
Los de clave pública (o asimétricos)
se caracterizan porque tienen dos claves una pública y otra privada.
La pública sirve para cifrar una información que solo podrá
descifrar aquel que posea la clave privada (el generador del criptosistema).
La privada sirve para descifrar el contenido de la información cifrada
con la clave pública, pero además si ciframos un mensaje
con la clave privada tendrán acceso a su contenido cualquier persona
que tenga la clave pública obteniendo autenticidad porque solo el
poseedor del criptosistema podrá cifrar un mensaje en clave privada
siempre y cuando este bien custodiada esta clave privada.
Los criptosistemas de clave pública son de coste algorítmico
muy elevado y muy difíciles de implementar.
1.- Teoría de la información
Entropía: medida del desorden. En un sistema de información
hay mucha entropía cuando hay mucha impredecibilidad.
La cantidad de información para el suceso xi
cuya probabilidad es P(xi) se define como -log P(xi)
La entropía es H = 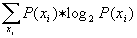 .
.
Podemos definir la cantidad de información que sobra de un lenguaje
como 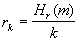 donde
rk es la redundancia del lenguaje (o índice del lenguaje)
real,
donde
rk es la redundancia del lenguaje (o índice del lenguaje)
real,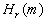 es la entropía
de los mensajes de longitud k. La redundancia absoluta es R =
log2(m) y la redundancia es la diferencia entre la absoluta
y la real D = R - rk.
es la entropía
de los mensajes de longitud k. La redundancia absoluta es R =
log2(m) y la redundancia es la diferencia entre la absoluta
y la real D = R - rk.
Un compresor (como el gzip) al comprimir un texto lo que hace es eliminar
toda la redundancia del lenguaje.
Si en vez de una variable para la probabilidad consideramos dos tales
como (X , Y) entonces definimos:
P( xi , y j ) es la probabilidad conjunta
al tratar los sucesos como independientes entre si.
P( xi / y j ) es la probabilidad condicionada
por el suceso y cuando son dependientes x e y.
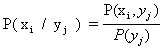
Y la entropía queda como:
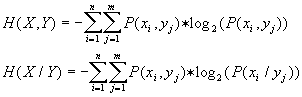
Ley de la entropía total
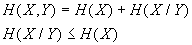
Si X e Y son independientes entonces H(X/Y) = H(X).
Definimos la cantidad de información de una variable frente
a otra como:
I(X,Y) = H(X) - H(X/Y)
Se define un criptosistema seguro de Shannon (o ideal) aquel que
cumpla la condición I(C,M) = 0, es decir que el hecho de conocer
C (mensaje cifrado) no nos dice nada sobre M (mensaje en claro). Para que
un sistema cumpla esto el cardinal de las claves debe ser como mínimo
igual al cardinal de los mensajes.
Definimos desinformación de un sistema criptográfico
como H(M /C).
Si H(M) = H (M / C) tendremos entonces un sistema seguro.
Definimos distancia de unicidad como la cantidad de mensaje
cifrado que necesitamos para descubrir la clave ( lo ideal es infinito).
Definimos confusión como el intento de ocultar la relación
directa entre C y M (K).
Se define como difusión como la repartición de
la redundancia por todo el texto cifrado (por transposición, es
decir cambiar las palabras de sitio).
2.- Matemática discreta
Aritmética modular
Es aquella aritmética que trabaja con conjuntos restringidos
a un tamaño ( llamado n, por ejemplo cuando utilizas un byte y a
255 le sumas 1 obtienes 0)
Dados a, b, n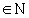
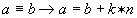 (a congruente
a b)
(a congruente
a b)
Máximo común divisor (Algoritmo de Euclides).
MCD (a, b)
g = a
h = b
mientras (h != 0)
{ x =
g %h
g = h
h = x
}
Si 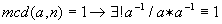 .
.
Denominaremos conjunto de residuos al conjunto formado por los
números 1..n-1
Denominaremos conjunto reducido de residuos (CRR) como al conjunto
de números primos entre si (es decir que no tienen divisores en
común).
La forma de hallar el cardinal de CRR es mediante la función
de Euler.
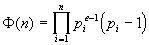 Donde p son los números primos en que se descompone el numero n
y e sus exponentes
Donde p son los números primos en que se descompone el numero n
y e sus exponentes
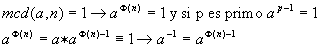
Exponenciación rápida
Dados dos numero a y b y dados b0, b1, b2,
b3,…, bn su correspondiente transcripción
en base 2 (binario).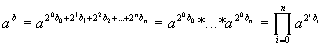
Esto quiere decir que para elevar un número "a" un exponente
tal que "b" no hay que multiplicar b veces sino como mucho log2 b.
expr (a ,b)
z = b
x = a
r = 1
mientras (z > 0)
{ si z%2 =1
r = r * x
x= x * x
z = z/2
}
Números primos
No existe ninguna formula para generar números primos, la única
forma de descomponer un número en sus factores primos es la fuerza
bruta. Solamente podemos comprobar si un numero es o no primo.
Método de Leman.
Sirve para saber si un número es primo.
En primer lugar se elige un número (a) de forma aleatoria que
sea menor que el número a testar (p).
Luego se calcula b tal y como sigue: 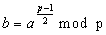 mediante la exponenciación rápida. Y si b es distinto a 1
o a p - 1 entonces no es primo y si no la incertidumbre de que sea primo
es de un 50%
mediante la exponenciación rápida. Y si b es distinto a 1
o a p - 1 entonces no es primo y si no la incertidumbre de que sea primo
es de un 50%
Se van realizando consecutivamente pruebas hasta que se encuentre que
no es primo o hasta que la incertidumbre sea pequeña.
¿Cómo generar un número primo aleatoriamente
que sea grande?
Se elige un número aleatorio del mismo tamaño de bits
del número a generar y se compara con una tabla de primos generada
anteriormente (de 2 a 1000)
Se define primos fuertes aquellos que cumplan los siguientes
criterios:
Sean p y q primos:
-
El máximo común divisor de p-1 y q-1 sea pequeño
-
P-1 y q-1 tengan algún factor primo grande (llamados p’ y q’).
-
P’-1 y q’-1 tengan algún factor primo grande.
-
P’+1 y q’+1 tengan algún factor primo grande.
Esto se utiliza como medidas anticriptoanálisis porque si n = p·
q Þ n no se puede factorizar si p y q
son primos fuertes.
Generación de números aleatorios
Se pueden conseguir mediante una función tal
que la relación entre los números generados sea tan oscura
para que no se pueda relacionarlos entre si y que dependiendo del número
del cual se parte sea distinta la secuencia generada.
Para iniciar esta función descrita anteriormente
se puede elegir la hora porque a no ser que se empiecen a contar dos funciones
sincronizadas se generara siempre una lista de números aleatorios.
La mejor manera de conseguir números realmente
aleatorios es sacando información de eventos físicos (tal
como el sonido, las moléculas de una determinada cosa, …).
3.- Criptografía clásica.
-
Varilla de mando: se consigue enrollando una tira de papel en un
bastón determinado y se escribe el mensaje en claro poniendo el
bastón en horizontal. Al desenrollar la tira de papel no se puede
leer el mensaje , pues esta cifrado. La clave es el diámetro de
la varilla.
-
Método César: se escribe el alfabeto y se escribe
debajo otro alfabeto desplazado tres letras. No es muy recomendable porque
la seguridad del algoritmo estriba en el secreto. Es un algoritmo de cifrado
por sustitución. Se puede implementar mediante C= (m+k) mod 256,
donde k es la clave (desplazamiento del alfabeto) .
-
Vigenere: es igual que el método César con el único
cambio que en vez de un alfabeto con desplazamiento se escriben varios
alfabetos que van utilizándose correlativamente. La clave
es el conjunto de números que desplazamos cada alfabeto.
-
Transposición: se trata de hacer un cambio de caracteres
cuya posición final viene dada por una permutación de un
número determinado de elementos. La clave es dicha permutación.
4.- Criptografía actual.
Criptografía de llave privada (simétricos).
DES.
La base del DES es la red de Feistel que consiste en separar
en dos bloques, izquierdo (L) y derecho (R) y se le aplica la siguiente
función:
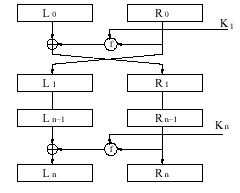 donde
donde
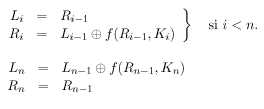 El algoritmo DES codifica bloques de 64 bits empleando
claves de 56 bits (un byte de paridad por clave). Es una red de Feistel
que efectúa dieciséis rondas , todo esto añadido a
dos permutaciones, una que se aplica al principio y otra al final. A partir
de la clave de 56 bits se sacan las subclaves de 48 bits.
El algoritmo DES codifica bloques de 64 bits empleando
claves de 56 bits (un byte de paridad por clave). Es una red de Feistel
que efectúa dieciséis rondas , todo esto añadido a
dos permutaciones, una que se aplica al principio y otra al final. A partir
de la clave de 56 bits se sacan las subclaves de 48 bits.
La función se compone de una permutación
de expansión, que convierte el bloque de 32 bits correspondiente
en uno de 48. Después realiza un or-exclusivo con el valor de la
clave i (48 bits) aplica ocho S-Cajas de 6*4 bits y efectúa una
nueva permutación.
Para descifrar se usa el mismo algoritmo pero utilizando
las 16 subclaves en orden inverso.
Actualmente, se ha mostrado que este algoritmo de
cifrado es sensible a ataques por fuerza bruta debido a la enorme potencia
de los computadores actuales. Pero, hay que resaltar que este algoritmo
desde el punto de vista teórico no tiene ninguna laguna.
Para solucionar este pequeño percance lo
que se puede hacer es aplicar este algoritmo varias veces tal y como sigue:
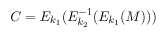
Triple- DES.
Este se basa en cifrar con una clave inicial el mensaje
en claro, luego al mensaje cifrado se descifra con otra clave, para terminar
con un cifrado con la clave inicial. Para descifrarlo es justo al revés.
Cifrados por bloques.
Al cifrar por bloques con un determinado algoritmo
nos encontramos un problema al querer cifrar una imagen o un texto muy
repetitivo ya que cogiendo un bloque determinado el mensaje cifrado en
si no nos aporta ninguna información sobre el texto en claro, pero
hay un determinado mensaje subliminal que no logramos ocultar.
He aquí un pequeño ejemplo:
Queremos cifrar el siguiente código
0++++++0
+0++++0+
++0++0++
+++00+++
Podemos observar que contiene una cierta información
subliminal.
Al cifrarlo con bloques de 8 nos podría quedar
así:
7******7
*7****7*
**7**7**
***77***
Como se observa queda en el texto cifrado un cierto mensaje subliminal.
Para evitar esto tenemos diferentes modos de cifrados por bloques.
Electronic Codeblook
Se subdivide la cadena que se quiere codificar en
bloques de tamaño adecuado y se cifran todos ellos utilizando la
misma clave. Este modo de cifrado es resistente a errores ya que si uno
de los bloques sufre una alteración el resto queda intacto.
Pero no acaba de ser muy bueno cuando el texto es
muy repetitivo.
Cipher Book Chaining Mode
Incorpora un mecanismo de retroalimentación
en cifrado por bloques. Esto significa que la codificación de bloques
anteriores condiciona la codificación del actual.
Esto se consigue efectuando una operación
XOR entre el bloque del mensaje que queremos cifrar y el último
mensaje cifrado obtenido.
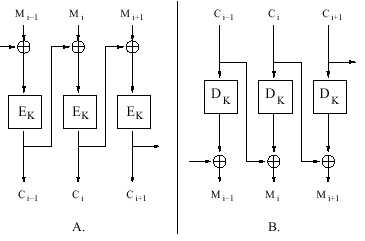 En la imagen superior la parte A es la de cifrado y la B de descifrado.
En la imagen superior la parte A es la de cifrado y la B de descifrado.
Para evitar que dos mensajes idénticos se codificasen de la
misma forma se crea un vector de inicialización.
Cipher Fedd-back
Este método no empieza a cifrar hasta que
no se ha completado el bloque a cifrar
Se carga un registro de desplazamiento con un vector
de inicialización. Codificamos el registro con un algoritmo simétrico
y cogemos sus n bits de mayor peso (donde n es el tamaño del bloque
resultante al cifrar). Luego desplazamos el registro n bits a la izquierda
y ponemos como bits de menor peso el mensaje obtenido.
Criptografía de llave pública
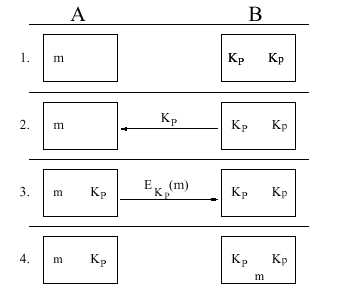
Esquema de como B le envia la clave publica a A y
este le envia un mensaje cifrado.
RSA.
Dados dos números e y d tales que uno sea
inverso del otro en aritmética modular en modulo Euler( n). Se define:
-
Llave pública como el par de números e y n.
-
Llave privada como el par de números d y n.
Para cifrar con el RSA simplemente se aplica la siguiente formula: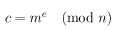
Para descifrar se aplica: 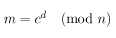
Para obtener n se eligen p y q dos números primos fuertes y
se multiplican obteniendo así n. Luego para calcular la función
de Euler la factorización de n en sus factores primos es trivial
(p*q).
Los inconvenientes del RSA son:
-
Es lento porque se eleva el mensaje en claro a un numero elevado
-
Se dispone de todo el material cifrado a gusto del consumidor porque cualquiera
puede cifrar con la clave publica un texto (el que quiera) y compararlo
con el original.
-
Ademas para que realmente sea seguro se necesita una clave de 1024 bits
porque con una clave de 512 bits se puede comparar con el DES teniendo
este una clave de 56 bits. .
6.- Estándares y aplicaciones criptográficas.
Firma digital
Vamos a plantearnos un pequeño problema.
Conocemos a dos individuos
Alicia y Eduardo y cada uno crea con un algoritmo RSA una clave publica
y otra privada. Pues bien nuestro objetivo es que Alicia le suministre
a Eduardo su clave publica para que pueda mandarle mensajes cifrados (Eduardo
a Alicia), y este reciba la clave de un modo seguro tal que sepa sin ninguna
duda que el propietario de esa clave publica es Alicia y no cualquier otra
persona.
Pues bien este "traspaso" de clave se podría
hacer de varias formas:
-
De un modo directo: Alicia queda en casa de Eduardo y le suministra la
clave. Pero existe un problema, ¿ y si Alicia vive en Estocolmo
y Eduardo en Perú?
-
Por teléfono: Alicia llama a Eduardo y tras una larga conversación
recordando momentos entrañables vividos juntos Alicia se asegura
que con quien esta hablando es con Eduardo, y esta le suministra la clave
publica. Pero, ¿ y si no hablan el mismo idioma o la llamada
es tan cara que prefieren no hablarse?.
-
Una posible solución es cifrar con la clave privada del emisor,
asi lo podrá descifrar quien tenga la clave pública
consiguiendo autenticidad. Pero hay un problema técnico ya que estos
algoritmos de clave pública son muy lentos y a medida que el mensaje
es mayor todavía más. Y también otro filosófico
¿cómo sabes que la clave pública de A es realmente
de A?
-
Mediante un e-mail con firma digital: este el sistema que vamos a estudiar
a continuación.
La firma digital no se aplica solo a mandar claves sino que también
a cualquier documento.
Para explicar lo que es una firma digital necesitamos saber primero
que son las funciones Hash o resumen.
Funciones
resumen.
Son funciones matemáticas las
cuales la entrada es un mensaje de cualquier tamaño y la salida
es un mensaje de un tamaño fijo (por eso lo de resumen).
También debe cumplirse que dado un mensaje
y su función resumen cualquier cambio (de posición de letra)
en el mensaje original producirá grandes cambios en su función
resumen asociada.
Dado un resumen debe ser difícil encontrar
su mensaje.
Algunos ejemplos de funciones
resumen o Hash: md5, sha1, sha2.
Una vez expuesto lo que son funciones resumen procedemos
a explicar la firma digital.
Queremos mandar un texto M firmado a una persona
y que el destinatario sepa que nosotros somos el autor. Para ello aplicamos
la función resumen a M obteniendo H(M) a este texto le aplicamos
un cifrado con la clave privada nuestra así solo él podrá
descifrarlo. Y lo adjuntamos el mensaje original. También adjuntamos
el objeto que contiene la clave publica del autor.
Pues bien cuando el destinatario reciba el mensaje
podrá ver su contenido y para verificarlo hará los siguientes
pasos:
-
Aplicará a M la función resumen (que ha aplicado también
el autor).
-
Descifrara con la clave pública del autor la segunda parte obteniendo
el resultado de la función resumen
Pues bien si el resultado de aplicar la función resumen a M es igual
al resultado de descifrar el churrito. Podemos asegurar que el texto no
ha sufrido modificaciones por terceras personas y que es el mensaje que
realmente nos quería mandar.
También podría plantearme el problema
que quiero autenticidad pero no quiero tampoco que terceras personas lean
el mensaje enviado.
Solución: podría cifrar todo el mensaje con la
clave pública del destinatario, pero eso tardaría mucho aún
en mensajes cortos.
Pues bien se establece el siguiente mecanismo:
-
Generamos un número aleatoriamente grande que tendremos que guardar
esta será nuestra clave de sesión.
-
Ciframos el mensaje que queremos enviar con la clave de sesión con
un algoritmo de clave privada.
-
Luego ciframos la clave de sesión con la clave pública del
destinatario, para que solo él pueda descifrar la clave que le permitirá
descifrar
el mensaje.
-
Todo esto se lo mandamos en un mensaje (clave cifrada y mensaje cifrado).
Luego una cosa a tener en cuenta la clave de sesión naturalmente
solo sirve para un mensaje sino el sistema puede fallar.
En la realidad se opta por un firmado y cifrado del mensaje. Es
importante decidir que hacemos primero si cifrar o firmar porque es importante.
Si optamos por un cifrado primero y luego lo firmamos
no establecemos el principio que nos planteamos , es decir una tercera
persona que interceptara este mensaje no conoce el mensaje pero sabe
que sea lo que sea esta firmado. Nuestro objetivo es ocultar toda la información
por eso es aconsejable firmarlo primero y resultado de firmarlo cifrarlo
así el interceptor no sabe nada del mensaje ni siquiera que esta
firmado porque se oculta detrás de el cifrado.
Autoridades ceritficadoras.
Pero continuamos con el mismo problema ¿cómo
sabe que la clave pública es realmente de Alicia?. No hay ningún
método fiable 100% pero podemos:
-
Mediante el contacto en persona: tal y como hablamos en la sección
anterior.
-
Mediante un notario (tal y como hacemos en la vida normalmente al comprar
una casa, un terreno, etc ...).
En Internet existen unas empresas que se dedican simplemente a emitir certificados
(los cuales tienes que pagarlos) para afirmar que realmente esa clave pública
es la tuya. Estas a su vez tienen certificados de empresas superiores,
y asi asi hasta llegar a una empresa que tiene la confianza de toda la
comunidad.
Alternativamente a las autoridades certificadoras existe un sistema
gratuito que se llama PGP.
Certificados X.509
El estándar X.509 sólo define la sintaxis por eso que
no está sujeto a ningún algoritmo. La estructura es la siguiente:
-
Versión
-
Número de serie
-
Identificador del algoritmo empleado para la firma digital
-
Nombre del certificador
-
Periodo de validez
-
Nombre del sujeto
-
Clave pública del sujeto
-
Identificador único de certificador
-
Identificador único de sujeto
-
Extensiones
-
Firma digital de todo lo anterior generada por el certificador.
![]()
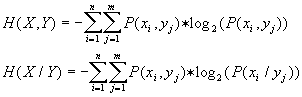
![]()
![]()
![]() (a congruente
a b)
(a congruente
a b)
![]() .
.
![]()
![]() mediante la exponenciación rápida. Y si b es distinto a 1
o a p - 1 entonces no es primo y si no la incertidumbre de que sea primo
es de un 50%
mediante la exponenciación rápida. Y si b es distinto a 1
o a p - 1 entonces no es primo y si no la incertidumbre de que sea primo
es de un 50%